Boolean Logic Diagrams

This is the OR gate for the Commutative Property showing that A + B = B + A meaning that the two inputs are added together. For example if A = 1 and B = 0 the output would be 1.

A	B	X
0	0	0
0	1	1
1	0	1
1	1	1

This is the AND gate for the Commutative Property which shows AB = BA meaning that the two input are multiplied together. For example if A = 1 and B=0 the output would be 0.

A	B	X
0	0	0
0	1	0
1	0	0
1	1	1

This is the AND gate for the Associative Property showing that (AB)C = A(BC) meaning that A and B are multiplied together to receive AB then C is added to the result to form (AB)C. For example if A = 1, B = 0, C = 1. AB would be 0 and then (AB)C would also receive a 0.

A	B	C	X
0	0	0	0
1	0	0	0
0	1	0	0
0	0	1	0
1	1	0	0
0	1	1	0
1	0	1	0
1	1	1	1

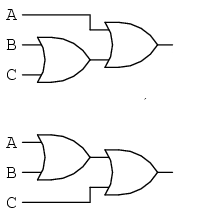
This is the OR gate for the Associative Property showing that (A+B) + C = A + (B+C) meaning that A and B are added together to receive A +B then C is added to A+B. For example if A = 1, B = 0, and C = 0. A+B would be 1 and A+B+C would be 1.

A	B	C	X
0	0	0	0
1	0	0	1
0	1	0	1
0	0	1	1
1	1	0	1
0	1	1	1
1	0	1	1
1	1	1	1

This the AND gate for the Distributive Property showing that A(B+C) = (AB) + (AC). meaning that B and C are added together to receive B+C then an A would me multiplied to B+C using an AND gate obtaining A(B+C). For example if A = 1, B = 0, and C = 1. 1+0=0*1=0 the final output would be 0.

A	B	C	X
0	0	0	0
1	0	0	0
0	1	0	0
0	0	1	0
1	1	0	1
0	1	1	0
1	0	1	1
1	1	1	1

This is the NOT gate for the Identity Property showing that A^1 = A or the inverse. For example if A = 1 the output would be 0 because it would become the inverse.

A	X
0	1
1	0

This is the NAND gate for the Complement Property showing that (A * B)^1. For example if A = 0 and B = 0 the output would be 1.

A	B	X
0	0	1
0	1	1
1	0	1
1	1	0

This is the NOR gate for the DeMorgan's Law showing that (A+B)^1. For example if A = 0 and B = 0 the output would be 1.

A	B	X
0	0	1
0	1	1
1	0	1
1	1	0